Fibonacci mit 1 Variable
12 Antworten
Ja, Sie können den Ausdruck in geschlossener Form verwenden:
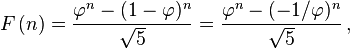
wo

Sie können den Ausdruck mit double berechnen und das Ergebnis auf die nächste Ganzzahl runden. Wegen der endlichen Genauigkeit der Fließkomma-Arithmetik gibt diese Formel eine falsche Antwort für groß genug n, aber ich denke, es wird in dem Fall funktionieren, wenn das Ergebnis in eine Java 32-Bit-Ganzzahl passt.
Bis zu einem gewissen Punkt, ja (obwohl in C, könnten Sie es in Java konvertieren - es würde viel hässlicher aussehen).
%Vor%welches produziert:
%Vor%: -)
Die eigentliche Frage ist natürlich: Warum willst du das?
Wenn Sie neugierig sind, wie es funktioniert, ist es wirklich ganz einfach. Die eine Variable ist tatsächlich in zwei Teile unterteilt, und diese zwei Teile behalten die individuellen Werte für die Fibonacci-Sequenz bei. Es ist immer noch technisch eine Variable, wir haben nur eine zusätzliche Struktur hinzugefügt, um unsere Ziele zu erreichen.
Die Antwort ist "Ja", aber vielleicht könnten Sie genauer sein.
Das erste Beispiel, an das ich denken könnte, ist die doppelte Rekursion (die zu einer exponentiellen Komplexität führt, nicht empfohlen):
%Vor%Angenommen, ein & gt; = 0 (Sie könnten eine Überprüfung dafür hinzufügen).
(Bearbeiten - verwendete die falsche Konvention von F (0) undefiniert, F (1) = 1)
Nach dem anfänglichen 1 1 ist es theoretisch möglich, einen Wert von dem vorherigen zu generieren (bis die Maschinengenauigkeit sich beißt) über:
Dabei ist PHI die in einem anderen Kommentar definierte Konstante:
static final double PHI = (1 + Math.sqrt(5))/2;
Sie können immer so etwas tun:
%Vor%Dies druckt ( auf ideone.com ):
%Vor% Dies verwendet nur eine explizite Variable, und es ist im Wesentlichen ein linearer nicht-rekursiver Algorithmus. Es muss jedoch gesagt werden, dass dies ein Missbrauch von String ist.
Das ist also böse, aber:
%Vor%Meine Maschine beginnt hier um die 38. Fibonacci-Nummer herum zu fallen.
Hier ist ein Beispiel in C #. Zeigt die ersten 100 Begriffe an. Das Verhältnis zwischen Termen im Fibonacci nähert sich dem Goldenen Schnitt (1,618033 ...), so dass ein einzelner variabler Ansatz einfach eine Multiplikation mit einer Konstante für jeden Term erfordert.
Yay Mathe!
%Vor%DAS PROGRAMM IST ZUM DRUCKEN BIS ZU 10 ZAHL, ABER SIE KÖNNEN SIE ÄNDERN.
%Vor%Das Programm hat einige Fehler im Import und in der Hauptaussage, aber der Körper ist vollständig korrekt
Hier ist der Java-Code der Fibonacci-Reihe mit einer Variablen.
Tags und Links java