Finden Sie, ob ein Winkel innerhalb von X Grad von einem anderen liegt
Ich brauche einen Algorithmus, um herauszufinden, ob ein Winkel innerhalb eines bestimmten Grades von einem anderen Winkel liegt.
Mein erster Gedanke war (a-x < b) && (a+x > b) , aber es schlägt fehl, wenn es mit Winkeln arbeiten soll, die von -179 bis 180 reichen.
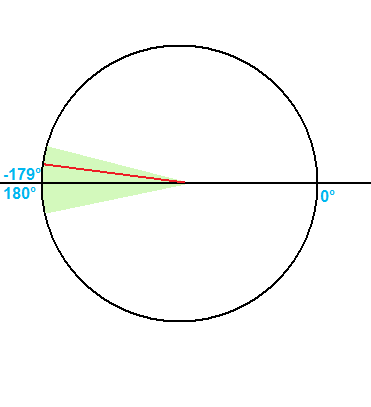
Im obigen Diagramm ist die Region (grün), um die der Winkel zwischen der negativen und der positiven Seite liegen muss. Wie kann ich feststellen, ob der Winkel (die rote Linie) in diesen Bereich fällt?
5 Antworten
Wie Marcel zu Recht betont, ist der Modulo bei negativen Zahlen potentiell problematisch. Was ist der Unterschied zwischen 355 und 5 Grad? Es könnte zu 350 Grad ausgearbeitet werden, aber 10 Grad ist wahrscheinlich, was die Leute erwarten. Wir machen folgende Annahmen:
- Wir wollen den kleinsten positiven Winkel zwischen zwei anderen Winkeln, also
0 <= diff <= 180; - wir arbeiten gradweise. Wenn Radiant, ersetzen Sie 360 für
2*PI; - Winkel können positiv oder negativ sein und außerhalb des Bereichs
-360 < x < 360liegen, wobei x ein Eingabewinkel und ist
- Reihenfolge der Eingabewinkel oder die Richtung der Differenz ist irrelevant.
Eingaben: Winkel a und b. Also ist der Algorithmus einfach:
- Normalisieren Sie a und b auf
0 <= x < 360; - Berechnen Sie den kürzesten Winkel zwischen den beiden normalen Winkeln.
Für den ersten Schritt, um den Winkel in den gewünschten Bereich zu konvertieren, gibt es zwei Möglichkeiten:
-
x >= 0: normal = x% 360 -
x < 0: normal = (-x / 360 + 1) * 360 + x
Die zweite dient dazu, jegliche Mehrdeutigkeit bei der Interpretation von Negativmodul-Operationen zu beseitigen. Also um ein funktionierendes Beispiel für x = -400 zu geben:
%Vor%dann
%Vor%Für die Eingänge 10 und -400 sind die normalen Winkel 10 und 320.
Jetzt berechnen wir den kürzesten Winkel zwischen ihnen. Um die Plausibilität zu überprüfen, muss die Summe dieser beiden Winkel 360 sein. In diesem Fall sind die Möglichkeiten 50 und 310 (zeichne es und du wirst es sehen). Um diese auszuarbeiten:
%Vor%Also für unser Beispiel:
%Vor% Sie werden normal1 + normal2 = 360 notieren (und Sie können sogar beweisen, dass dies der Fall ist, wenn Sie möchten).
Zuletzt:
%Vor%oder 50 in unserem Fall.
Für einen Radius von 1 ist der Abstand zwischen den Linienendpunkten 2sin ((ab / 2).) Wirf also die 2 weg, da du nur an einem Vergleich interessiert bist, und vergleiche sin (x / 2) mit sin (( ab) / 2) Die trigonometrischen Funktionen sorgen für den gesamten Wickel.
Tags und Links algorithm language-agnostic circle angle