advertising
Wenn Sie dies als Binomialparameter behandeln, können Sie eine Bayessche Schätzung vornehmen. Wenn Ihr Prior bei ctr einheitlich ist (eine Beta-Verteilung mit Parametern (1,1)), dann ist Ihr posterior Beta (1 + # Klick, 1 + # Impressionen- # Klick). Ihr hinteres Mittel ist # click + 1 / # impressions + 2, wenn Sie eine einzige zusammenfassende Statistik dieses hinteren Bereichs wünschen, aber Sie wahrscheinlich nicht, und hier ist warum:
Ich weiß nicht, mit welcher Methode Sie feststellen, ob ctr hoch genug ist, aber sagen wir, Sie interessieren sich für alles mit ctr & gt; 0.9. Sie können dann die kumulative Dichtefunktion der Beta-Verteilung verwenden, um zu sehen, welcher Anteil der Wahrscheinlichkeitsmasse über der Schwelle von 0,9 liegt (dies ist nur 1 - der cdf bei 0,9). Auf diese Weise wird Ihre Schwelle aufgrund der begrenzten Stichprobengröße natürlich Unsicherheit über die Schätzung beinhalten.
Es gibt viele Möglichkeiten, dieses Konfidenzintervall zu berechnen. Eine Alternative zum Wilson-Score ist das Clopper-Perrson-Intervall, das ich in Tabellenkalkulationen nützlich fand.
Wo
- %code% ist die Inverse Beta-Distribution
- %code% ist der Konfidenzniveaufehler (z. B. für 95% -Konfidenzniveau, Alpha ist 5%)
- %code% ist die Anzahl der Stichproben (z. B. Impressionen)
- %code% ist die Anzahl der Erfolge (z. B. Klicks)
In Excel wird eine Implementierung für %code% von der %code% Formel bereitgestellt.
In Google Tabellen gibt es keine gleichwertige Formel für B (), aber eine benutzerdefinierte Funktion für Google Apps Script kann aus der JavaScript Statistical Library (z. B. Suche nach github für jstat) angepasst werden
Sie benötigen wahrscheinlich eine Darstellung des Konfidenzintervalls für Ihre geschätzte ctr. Wilson-Score-Intervall ist ein guter Versuch.
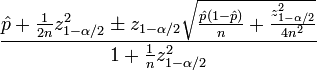
Sie benötigen die folgenden Statistiken, um den Konfidenzwert zu berechnen:
- %code% ist der beobachtete ctr (Bruchteil von #klicked vs #impressions)
- %code% ist die Gesamtzahl der Impressionen
- %code% α / 2 ist das %code% -Quantil der Standardnormalverteilung
Eine einfache Implementierung in Python ist unten gezeigt, ich verwende %code% (1-α / 2) = 1.96 was einem 95% Konfidenzintervall entspricht. Ich habe 3 Testergebnisse am Ende des Codes angehängt.
%Vor%Jetzt können Sie einen Schwellenwert für die Verwendung des berechneten Konfidenzintervalls einrichten.
%Vor%Wenn wir ein ctr (click through rate) -Modell trainieren, müssen wir manchmal die reale ctr aus den History-Daten berechnen, so wie dies
%Vor%Wenn die Anzahl der Impressions zu klein ist, ist das berechnete ctr nicht real. Daher legen wir immer einen Schwellenwert fest, um die ausreichend großen Impressionen herauszufiltern.
Aber wir wissen, dass die höheren Eindrücke, das höhere Vertrauen für die ctr. Dann ist meine Frage: Gibt es eine impressions-normalisierte Statistikmethode zur Berechnung der ctr?
Danke!